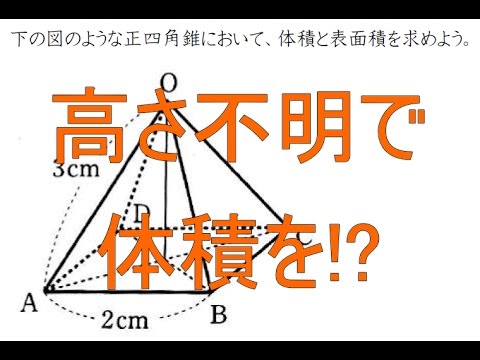
《四角錐の高さの求め方》 (底面は一辺が12cmの正方形) 四角錐の体積=底面積×高さ× より 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)と
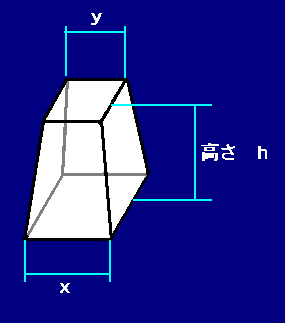
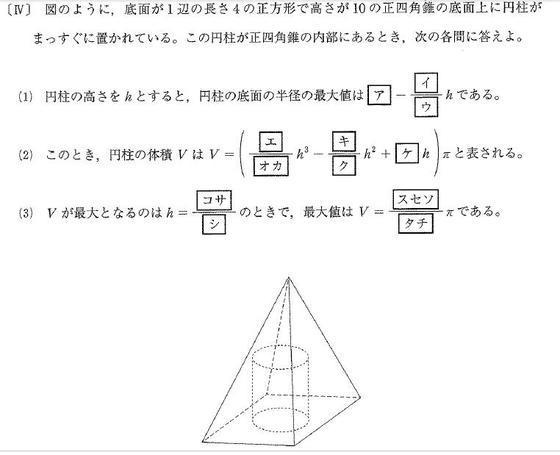
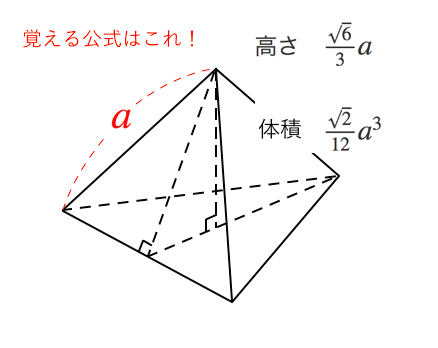
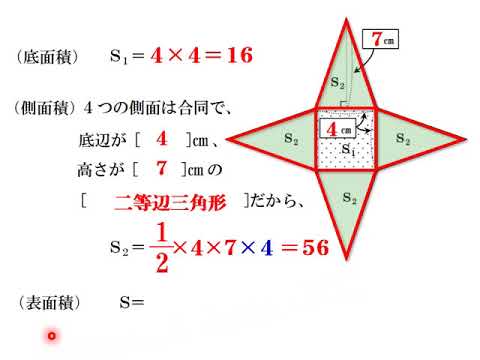
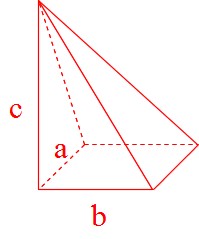
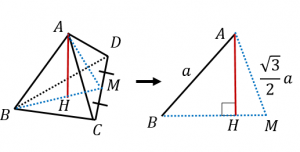
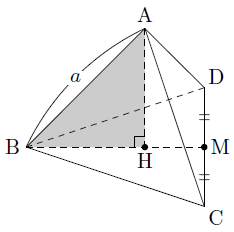
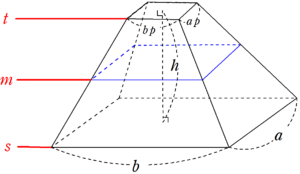
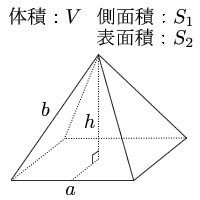
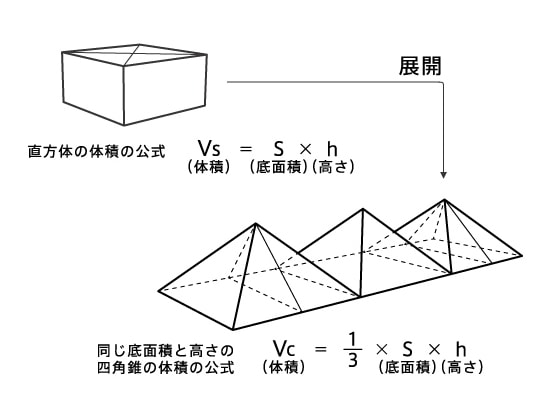
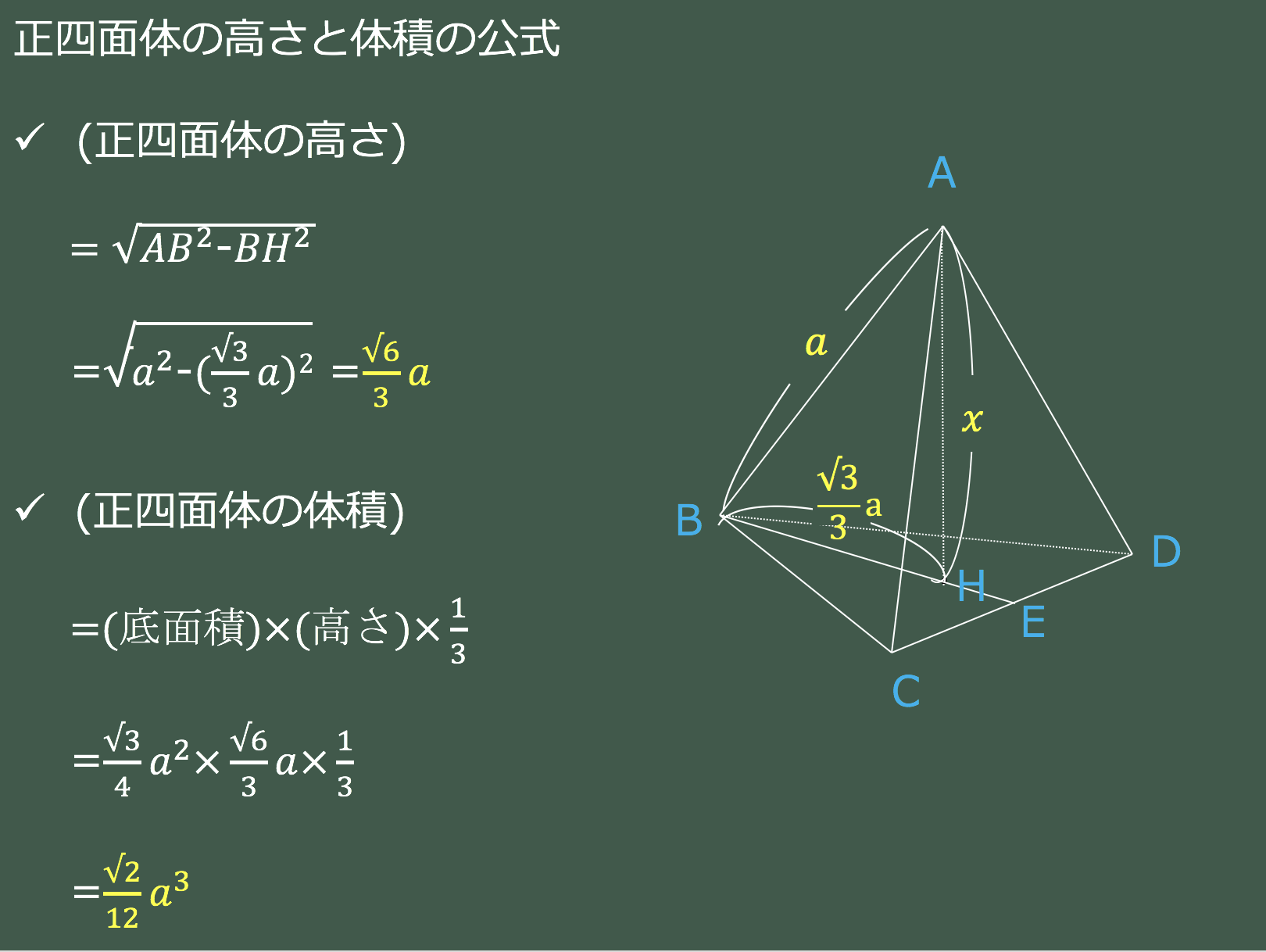
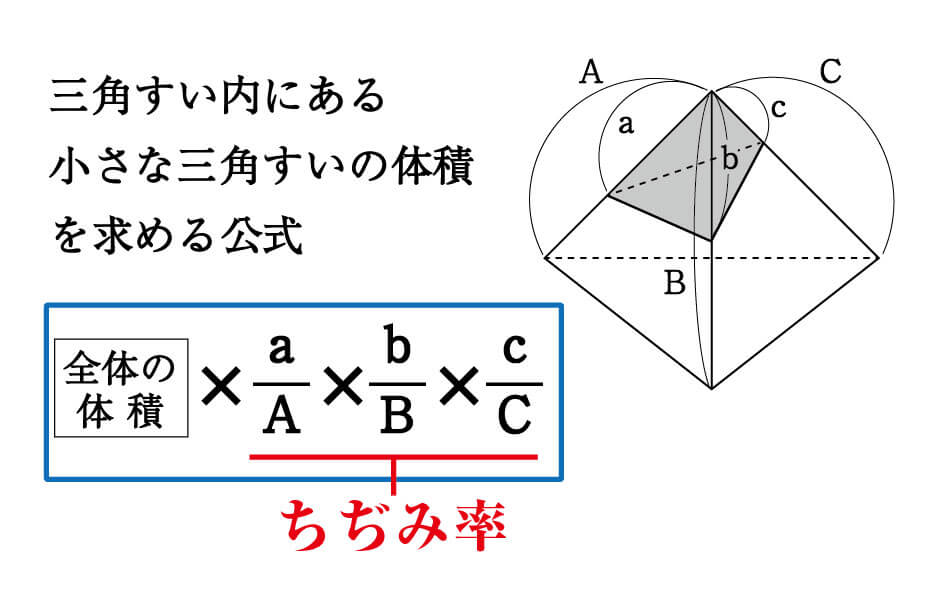
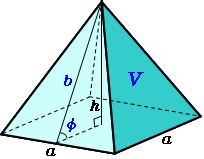
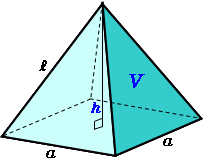
正四角錐 高さ 公式-正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。 底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。 1/3 a²h つまり、 (底辺の1辺)×(底辺の1辺)×(正四角錐の高さ)÷3 ってことだね。 一辺が 2の正四面体 abcdの高さの求め方を教えてください。 a から底面に垂線をおろし、高さをah とします。直線cd の中点をm とします。 ah=absin∠abm で求められるらしいのですが、どうしてこの式になるのかがわかりません。
正四角錐 高さ 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 | ||
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 | ||
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  |  |
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「正四角錐 高さ 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |
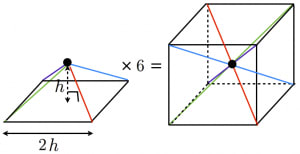
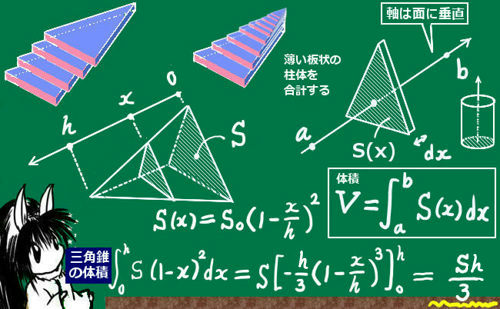
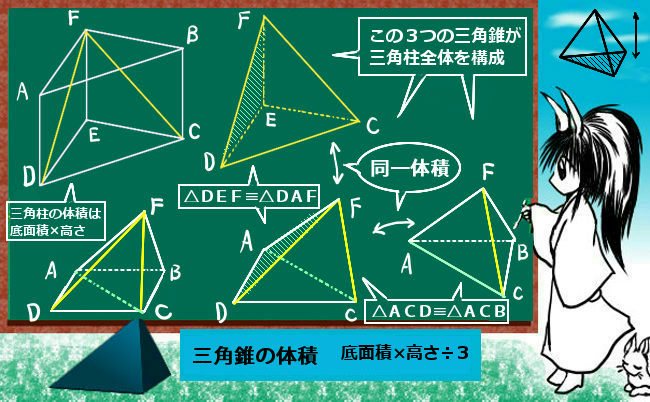
OGは0Aに平行で長さが3分の1 の関係があることがわかります。 すなわち、AGは重心O点を通ることがわかり、 線分AGが点Oで3:1に分割されることもわかります。 すなわち、 三角錐の重心Oの位置は、その高さの4分の1になる まとめ:正四角錐の体積の求め方も大丈夫! 正四角錐の体積の公式はどうだった? ? 底面積×高さ×1/3 という計算をゆっくりしてみてね。 テスト前に復習しておくと心強いかも! そん
Incoming Term: 正四角錐 高さ 公式,




0 件のコメント:
コメントを投稿